Question

A 4 m^3 metal block is suspended using a cable in salt water with density 1030 kg/m^3. Tension on the cable is 42600N. What is the weight of the block. What is the density of the block?

Answer 1

The density of the block is 1113.216 kilograms per cubic meter.

The weight of the block is 43669.237 newtons.

Step-by-step explanation:

According to the Archimedes' Principle, the drag force experimented by the metal block is equal to the weight of the volume of water displace by the block. Besides, the block has a weight that cannot be neglected and experiments a tension from the cable. Given that the metal block is suspended, then we could consider that block is at rest.

From Newton's Laws of Motion we obtain the following equation of equilibrium:

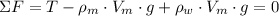`\Sigma F = T-\rho_(m)\cdot V_(m)\cdot g + \rho_(w)\cdot V_(m)\cdot g = 0` (1)

Where:

`T` - Tension on the cable, measured in newtons.

`\rho_(w)`,
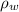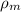`\rho_(m)` - Densities of salt water and the metal block, measured in kilograms per cubic meter.

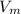`V_(m)` - Volume of the metal block, measured in cubic meters.

`g` - Gravitational acceleration, measured in meters per square second.

If we know that
`T = 42600\,N`,
`\rho_(w) = 1030\,(kg)/(m^(3))`,
`V_(m) = 4\,m^(3)`,
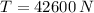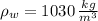`g = 9.807\,(m)/(s^(2))`, then the density of the block is:

`T+\rho_(w)\cdot V_(m)\cdot g = \rho_(m)\cdot V_(m)\cdot g`

`\rho_(m) = (T+\rho_(w)\cdot V_(m)\cdot g)/(V_(m)\cdot g)`

`\rho_(m) = (42600\,N+\left(1030\,(kg)/(m^(3)) \right)\cdot (4\,m^(3))\cdot \left(9.807\,(m)/(s^(2)) \right))/((4\,m^(3))\cdot \left(9.807\,(m)/(s^(2)) \right))`

`\rho_(m) = 1113.216\,(kg)/(m^(3))`

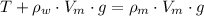
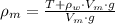
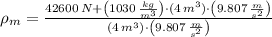
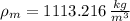
The density of the block is 1113.216 kilograms per cubic meter.

Lastly, the weight of the block (
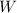`W`), measured in newtons:

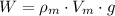`W = \rho_(m)\cdot V_(m)\cdot g` (2)

`W = \left(1113.216\,(kg)/(m^(3))\right)\cdot (4\,m^(3)) \cdot \left(9.807\,(m)/(s^(2)) \right)`

`W = 43669.237\,N`

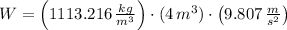
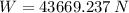
The weight of the block is 43669.237 newtons.