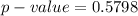Question

Assume that the readings are a random sample from a population that follows the normal curve. We perform a t-test to see whether the scale is properly calibrated. Find the corresponding P-value for this test..

Answer 1

Complete Question

Each of the following hypothetical data set represents some repeated weighing of a standard weight that is known to have a mass of 100 g. Assume that the readings are a random sample from a population that follows the normal curve. We perform a t-test to see whether the scale is properly calibrated. Find the corresponding P-value for this test..

The data in grams are

100.02 , 99.98 , 100.03

Answer:

The p-value is
`p-value =0.5798`

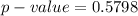
Explanation:

Generally the sample mean of the given data is mathematically represented as

`\= x = (100.02 + 99.98 + 100.03 )/(3)`

`\= x =100.03 \ g`

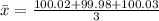
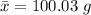
Generally the standard deviation is mathematically represented as

`s = \sqrt{(\sum [x_i - \= x]^2 )/(n-1) }`

=>
`s = \sqrt{([ 100.02 - 100.01]^2+ [ 99.98 - 100.01]^2+[ 100.03 - 100.01]^2 )/(3-1) }`

=>
`s = 0.02645`

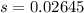
The null hypothesis is
`H_o : \mu = 100`

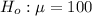
The alternative hypothesis is
`H_a : \mu \\e 100`

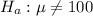
Generally the degree of freedom is mathematically represented as

`df = n - 1`

=>
`df = 3 - 1`

=>
`df = 2`

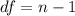
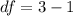
Generally the test statistics is mathematically represented as

`t = (\= x - \mu )/((s)/(√(n) ) )`

=>
`t = ( 100.01 - 100 )/((0.02645)/(√(3) ) )`

=>
`t = 0.655`

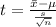
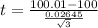
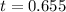
From the t distribution table the probability corresponding to the t to the right of the bell curve at a degree of freedom of
`df = 2`

`P( T > 0.655 ) = 0.2899`

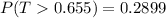
Generally the p-value for this two tailed test is mathematically represented as

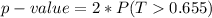
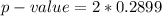
`p-value = 2 * P(T > 0.655)`

=>
`p-value = 2 * 0.2899`

=>
`p-value =0.5798`