Answer:
Hay 50 latas en total que tocan el fondo de la caja.
Explanation:
Una caja de cartón es representada por un cuadrilátero, cuyas caras son rectángulos. Si la caja esta ocupada por completo, entonces la cantidad total de latas es representada por la siguiente expresión:
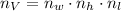 (1)
(1)
Donde:
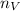 - Total de latas de atún, adimensional.
- Total de latas de atún, adimensional.
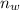 - Cantidad de latas de atún a lo ancho de la caja, adimensional.
- Cantidad de latas de atún a lo ancho de la caja, adimensional.
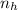 - Cantidad de latas de atún a lo alto de la caja, adimensional.
- Cantidad de latas de atún a lo alto de la caja, adimensional.
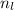 - Cantidad de latas de atún a lo largo de la caja, adimensional.
- Cantidad de latas de atún a lo largo de la caja, adimensional.
De acuerdo con el enunciado, tenemos las siguientes relaciones:
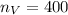 (2)
(2)
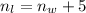 (3)
(3)
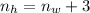 (4)
(4)
Si aplicamos estas fórmulas a (1), tenemos el siguiente polinomio de tercer orden:
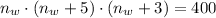

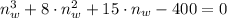
Este polinomio se puede resolver por vía analítica por el Método de Cardano o por vía numérica, sus raíces son:
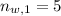 ,
,
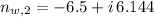 ,
,
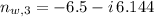
En consecuencia, la única solución válida es
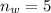 y las variables restantes son por (3) y (4):
y las variables restantes son por (3) y (4):
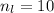 y
y
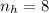
La cantidad de latas que tocan el fondo de la caja es igual al producto de la cantidad de latas a lo largo de la caja y la cantidad de latas a lo ancho de la caja, es decir:
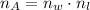 (5)
(5)
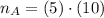
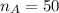
Hay 50 latas en total que tocan el fondo de la caja.