Answer:
The coordinates of B' and C' are
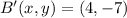 and
and
 , respectively.
, respectively.
Explanation:
From the Linear Algebra, we define the translation of a given point as:
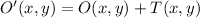 (1)
(1)
Where:
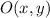 - Original point, dimensionless.
- Original point, dimensionless.
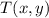 - Translation vector, dimensionless.
- Translation vector, dimensionless.
 - Translated point, dimensionless.
- Translated point, dimensionless.
If we know that
 and
and
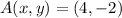 , then the translation vector is:
, then the translation vector is:
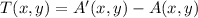 (2)
(2)
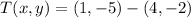
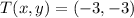
If we know that
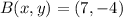 ,
,
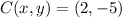 and
and
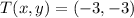 , then the translated points are, respectively:
, then the translated points are, respectively:
 (3)
(3)
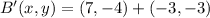
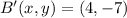
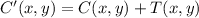
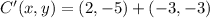

The coordinates of B' and C' are
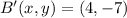 and
and
 , respectively.
, respectively.