Answer:
Podemos determinar la velocidad del automóvil mediante diferencias sucesivas tanto en el dominio del tiempo como en el dominio de la posición:
Dominio del tiempo
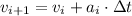
Dominio de la posición
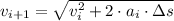
Explanation:
En este caso, es necesario tener una función que represente a esta en función del tiempo o de la posición si nos basamos en las definiciones diferenciales de aceleración (
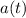 ), medida en metros por segundo al cuadrado, es:
), medida en metros por segundo al cuadrado, es:
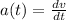 (1)
(1)
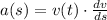 (2)
(2)
Donde:
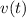 - Velocidad del automóvil, medida en metros por segundo.
- Velocidad del automóvil, medida en metros por segundo.
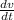 - Primera derivada de la velocidad con respecto al tiempo, medida en metros por segundo.
- Primera derivada de la velocidad con respecto al tiempo, medida en metros por segundo.
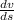 - Primera derivada de la velocidad con respecto a la posición, medida en
- Primera derivada de la velocidad con respecto a la posición, medida en
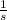 .
.
A continuación, analizamos cada ecuación:
Eq. 1
Procedemos a despejar la diferencial de velocidad e integramos la expresión resultante:
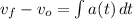 (3)
(3)
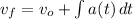
Podemos obtener aproximaciones sucesivas al discretizar la ecuación anterior, es decir:
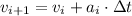 (3b)
(3b)
Eq. 2
Procedemos a despejar la velocidad e integramos la expresión resultante:
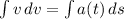 (4)
(4)
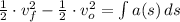
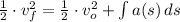
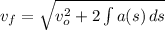
Podemos obtener aproximaciones sucesivas al discretizar la ecuación anterior, es decir:
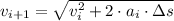 (4b)
(4b)