Question

Suppose 30% of the U.S. population has green eyes. If a random sample of size 1200 U.S. citizens is drawn, then the probability that less than 348 U.S. citizens have green eyes is _______.

Answer 1

P(X is less than 348) = 0.2148

Explanation:

Given that:

Sample proportion (p) = 0.3

Sample size = 1200

Let X be the random variable that obeys a binomial distribution. Then;

`X \sim Bin(n = 1200,p =0.3)`

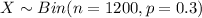
The Binomial can be approximated to normal with:

`\mu = np = 1200 * 0.3 \\ \\ \mu= 360`

`\sigma = √(np(1-p) ) \\ \\ \sigma = √(1200 * (0.3)(1-0.3) ) \\ \\ \sigma = 15.875`

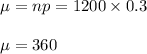
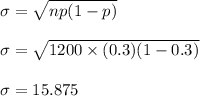
To find:

P(X< 348)

So far we are approximating a discrete Binomial distribution using the continuous normal distribution. 348 lies between 347.5 and 348.5

Normal distribution:

x = 347.5,
`\mu` = 360,
`\sigma` = 15.875

Using the z test statistics;

`z = (x - \mu)/(\sigma)`

`z = (347.5 - 360)/(15.875)`

`z = (-12.50)/(15.875)`

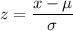
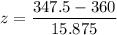
z = -0.7874

z ≅ - 0.79

The p-value for P(X<347.5) = P(Z < -0.79)

From the z tables;

P(X<347.5) = 0.2148

Thus;

P(X is less than 348) = 0.2148