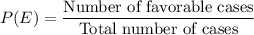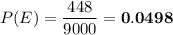Question

What is the probability that a randomly chosen four-digit integer (no leading zeros) has distinct digits and ends with the digit 7? For example, 1237 qualifies for the event space but 1227 does not.

All of the possible answers are rounded to four decimal digits.

a. 0.3484
b. 0.0448
c. 0.0498
d. 0.0720

Answer 1

c. 0.0498

Explanation:

First of all, let us find the number of four digit numbers possible.

There are 4 digits and let us have a look at the possibility of each digit.

Number of possible options for Unit's digit = 10

Number of possible options for ten's digit = 10

Number of possible options for hundred's digit = 10

Number of possible options for thousand's digit = 9 (because 0 can not be there to make it a 4 digit number)

Total number of possible outcomes =
`10* 10* 10* 9 = \bold{9000}`

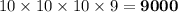
As per the given condition, unit's digit is 7.

So, number of possible options for unit's digit = 1

Number of possible options for thousand's digit = 8 (7 and 0 can not be there to make it a 4 digit number)

Number of possible options for hundred's digit = 8 (7 and one digit used in thousand's place can not be there)

Number of possible options for ten's digit = 7 (7, two digits used at thousand's and hundred's places)

Number of possible outcomes as per given conditions =
`1* 8* 8* 7 = \bold{448}`

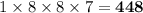
Formula for probability of an event E can be observed as:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

`P(E) = (448)/(9000) =\bold{0.0498}`