Question

A air traffic control system is tracking two fighter jets, both of which are flying at the same altitude and their directed distance is measured in kilometers. If they have coordinates of (4, 150°) and (2, 195°), find the distance between the two jets.

Answer 1

The distance between the two jets is approximately 2.947 kilometers.

Explanation:

From the statement we know the location of each jet in polar coordinates, which are defined by the following notation:

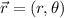`\vec r = (r, \theta)` (1)

Where:

`r` - Distance of the jet from the origin, measured in kilometers.

`\theta` - Angle of the jet with respect to the east direction, measured in sexagesimal degrees.

To transform polar coordinates into rectangular coordinates, we use the following expressions:

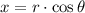`x = r\cdot \cos \theta` (2)

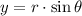`y = r\cdot \sin \theta` (3)

And lastly, we determine the distance between the two jets (
`d`), measured in kilometers, by the Pythagorean Theorem:

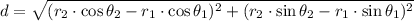`d = \sqrt{(r_(2)\cdot \cos \theta_(2)-r_(1)\cdot \cos \theta_(1))^(2)+(r_(2)\cdot \sin \theta_(2)-r_(1)\cdot \sin \theta_(1))^(2)}` (4)

If we know that
`r_(2) = 4\,km`,
`\theta_(2) = 150^(\circ)`,
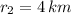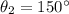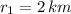`r_(1) = 2\,km` and
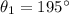`\theta_(1) = 195^(\circ)`, the distance between the two jets is:

`d = \sqrt{[(4\,km)\cdot \cos 150^(\circ) -(2\,km)\cdot \cos 195^(\circ)]^(2)+[(4\,km)\cdot \sin 150^(\circ) -(2\,km)\cdot \sin 195^(\circ)]^(2)}`

`d \approx 2.947\,km`

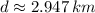
The distance between the two jets is approximately 2.947 kilometers.