Answer:
Following are the solution to the given point:
Explanation:
Grade of students:
Grade of student:
In point a:
Grade of
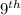 students:
students:
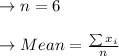
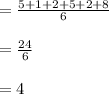
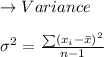
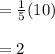

Since the Grade of
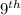 student's variance is higher than
student's variance is higher than
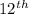 grade,
grade,
In point b:
Please find the attached file.
The plot above shows that the student of the ninth grade is spread more widely, as the student from 0-8 to 12 is from 0-4.