Complete Question
Leicester City Fanstore (LCF) will be selling the "new season jersey" for the 2018-2019 season. The regular price of the jersey is $80. Each jersey costs $40. Leftover jerseys will be sold at the end of the season (or later) at $30. Since jerseys are produced in China and lead time is long, Puma wants LCF to decide the quantity right now (December 2017).
a. After some analysis using historic data, LCF expects that the demand will follow a Normal distribution with a mean 40,000 and a standard deviation of 8,000 due to uncertainty in team performance. How many jerseys should LCF order?
b. If a customer cannot buy the jersey from LCF (in the case of a stock-out), they may leave the store disappointed and use other channels (such as Puma stores or puma.com) in future. LCF thinks that the lost customer goodwill is around $10. Should LCF change their decision in part (a)? If yes, please state the number of jerseys LCF should order.
c. Please state whether the following statement is always true, and give a brief explanation. If
 , the news vendor solution is the mean.
, the news vendor solution is the mean.
Answer:
a
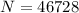
b
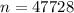
c
Yes it is always true
Step-by-step explanation:
From the question we are told that
The regular price of the jersey is

The cost of producing a jersey is
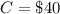
The left-over price of the jersey is

The mean is

The standard deviation is

The cost of lost customer goodwill is
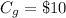
Generally the fund that LCF will loss for one jersey if they order for too many jersey (i.e more than they need )is mathematically represented

=>

=>
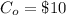
Generally the fund that LCF will loss for one jersey if they order lesser amount jersey (i.e less than they need )is mathematically represented
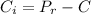
=>
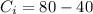
=>
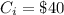
Generally the critical ratio is mathematically represented as
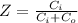
=>
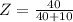
=>
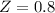
Generally the critical value of
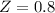 to the right of the normal curve is
to the right of the normal curve is

Generally the optimal quantity of jersey to order is mathematically represented as
![N = \mu * [z * \sigma]](https://img.qammunity.org/2021/formulas/mathematics/college/iute6607xwwtcgnxo16zs3xxbb1cyfcfpl.png)
=>
![N = 40000 * [0.841 * 8000]](https://img.qammunity.org/2021/formulas/mathematics/college/5jnewh0gyyiel7475e1mpafg0cyubguxid.png)
=>
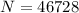
Considering question b
Generally considering the factor of customer goodwill the fund that LCF will loss for one jersey if they order lesser amount jersey (i.e less than they need )is mathematically represented as
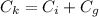
=>
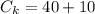
=>
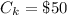
Now the critical ratio is mathematically represented as

=>
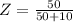
=>
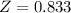
Generally the critical value of
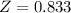 to the right of the normal curve is
to the right of the normal curve is
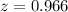
Generally the optimal quantity of jersey to order is mathematically represented as
![n = \mu * [z * \sigma]](https://img.qammunity.org/2021/formulas/mathematics/college/61qc4ibhv0vv3uyq8nqhl9cdg0btr4q25k.png)
=>
![n = 40000 * [0.966 * 8000]](https://img.qammunity.org/2021/formulas/mathematics/college/n6tyx643mpokb8vjfsbg88yblqhmwkz3eg.png)
=>
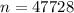
Considering question c
When
 then
then
The critical ratio is mathematically represented as
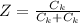
=>
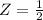
=>
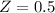
Generally the critical value of
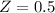 to the right of the normal curve is
to the right of the normal curve is
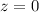
So
The optimal quantity of jersey to order is mathematically represented as
![n = \mu * [z * \sigma]](https://img.qammunity.org/2021/formulas/mathematics/college/61qc4ibhv0vv3uyq8nqhl9cdg0btr4q25k.png)
=>
![n = 40000 * [0* 8000]](https://img.qammunity.org/2021/formulas/mathematics/college/hdnri8lktqbxj9s56pknvy1eewrzedbgvl.png)
=>
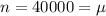
Hence the statement in c is true