Question

In a sample of 41 temperature readings taken from the freezer of a restaurant, the mean is 29.7 degrees and the population standard deviation is 2.7 degrees. What would be the 80% confidence interval for the temperatures in the freezer?

Answer 1

Answer:
`=(29.1596\text{ degrees},\ 30.2404\text{ degrees})`

Explanation:

Given: Sample size: n = 41

Sample mean
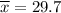`\overline{x}= 29.7` degrees

Population standard deviation
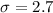`\sigma=2.7` degrees

Confidence level (c) = 80% =0.80

Significance level (a) = 1- c = 1-0.80 = 0.20

z-score for 80% confidence level : z = 1.2816 [from z-table]

Confidence level for population mean :-

`\overline{x}\pm z(\sigma)/(√(n))`

`=29.7\pm ( 1.2816)(2.7)/(√(41))`

`=29.7\pm ( 1.2816)(2.7)/(6.403124)`

`=29.7\pm ( 1.2816)(0.42167)`

`=29.7\pm 0.5404`

`=(29.7-0.5404,\ 29.7+0.5404)`

`=(29.1596,\ 30.2404)`

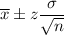
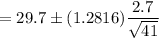
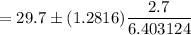
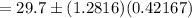
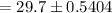
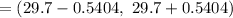
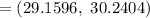
Hence, 80% confidence interval for the temperatures in the freezer
`=(29.1596\text{ degrees},\ 30.2404\text{ degrees})`