Answer:
8. Number of student tickets = 460
Number of teacher tickets = 100
9. Speed of plane = 727.5 km/hr
Speed of wind = 48.5 km/hr
Explanation:
8.
Let number of students' tickets =

Let number of teachers' tickets =

Total number of tickets = 480
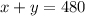 ...... (1)
...... (1)
Price for one student's ticket = $1
Price for one teacher's ticket = $5
Total money collected by the tickets = $560
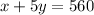 ...... (2)
...... (2)
Subtracting (1) from (2):

By equation (1):
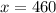
Number of student tickets = 460
Number of teacher tickets = 100
9.
Let the speed of airplane in still air =
 km/hr
km/hr
Let the speed of air =
 km/hr
km/hr
Total distance = 5432 km
Time taken with the wind = 7 hours.
Speed with the wind =
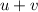 km/h
km/h
Time taken against the wind = 8 hours.
Speed with the wind =
 km/h
km/h
Using the formula:
Distance = Speed
 Time
Time
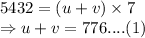

Adding (1) and (2):
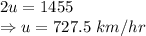
By equation (1):
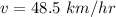
Speed of plane = 727.5 km/hr
Speed of wind = 48.5 km/hr