Given:
Total students = 6,000
Students taking honors courses = 1,500
Students preferring basketball = 1,800
Students in both = 450
To find:
Whether the two events "taking honors courses" and "preferring basketball" are independent or not?
Solution:
Let as consider the following events.
A : Taking honors courses
B : Preferring basketball
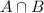 : Both
: Both
We know that,
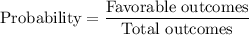
Using this formula, we get
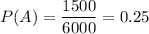
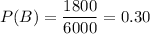
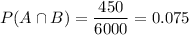
Two evens are independent if
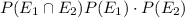
Now,
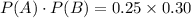
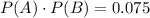
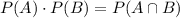
So, the events A and B are intendent because
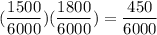
Therefore, the correct option is D.