Question

A standing wave measures 0.25 m between nodes and its frequency is 1500 hz. what is the standing wave's speed?

380 m/s
750 m/s
1500 m/s

Answer 1

`750\; {\rm m\cdot s^(-1)}`.

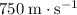Step-by-step explanation:

The distance between two adjacent nodes of a standing wave is equal to one-half (that is,
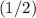`(1/2)`) the wavelength of this wave.

Let
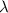`\lambda` denote the wavelength of the standing wave in this question. The distance between two nodes of this wave is
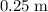`0.25\; {\rm m}`, meaning that
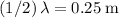`(1/2)\, \lambda = 0.25\; {\rm m}`. Thus,
`\lambda = 2 * 0.25\; {\rm m} = 0.50\; {\rm m}`.

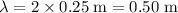Given that
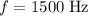`f = 1500\; {\rm Hz}` is the frequency of the waves that formed this standing wave, the speed of these waves would be:

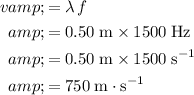`\begin{aligned}v &= \lambda\, f \\ &= 0.50\; {\rm m} * 1500\; {\rm Hz} \\ &= 0.50\; {\rm m} * 1500\; {\rm s^(-1)} \\ &= 750\; {\rm m\cdot s^(-1)}\end{aligned}`.