Answer:
m<T =
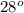 , m<M =
, m<M =
 and m<Z =
and m<Z =

Explanation:
From the given ∆TMZ, let the measure angle T be represented by T.
So that,
m<M = 2T + 6°
m<Z = 5T - 50°
Sum of angles in a triangle =
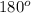
T + (2T + 6°) + (5T - 50°) =
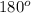
8T -
 =
=
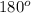
8T =
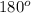 +
+

=

T =
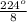
=
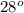
Therefore,
i. m<T =
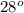
ii. m<M = 2T + 6°
= 2 x
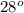 + 6°
+ 6°
=

m<M =

iii. m<Z = 5T - 50°
= 5 x
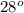 - 50°
- 50°
=
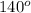 - 50°
- 50°
=

m<Z =
