Question

A rectangle has length 4 inches and width 2 inches. If the length and width of the rectangle are each reduced by 50 percent, by what percent will the area of the rectangle be reduced?

Answer 1

Answer: 25%

Explanation:

Given: A rectangle has length 4 inches and width 2 inches.

Area = Length x width

= 4 inches x 2 inches

= 8 square inches

If length is reduced by 50% , then length
`=0.5*4=2\text{ inches}`

If width is reduced by 50% , then length
`=0.5*2=1\text{ inch}`

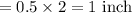
Reduced area = (reduced length) x (reduced width)

= 2 inches x 1 inch

= 2 square inches

The percentage of the area of the rectangle be reduced :-

`\frac{\text{Reduced area}}{\text{Original area}}*100 \\\\=(2)/(8)*100\% \\\\=25\%`

Hence, the percent of the area of the rectangle be reduced = 25%