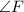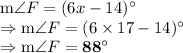Question

In ΔFGH, \text{m}\angle F = (6x-14)^{\circ}m∠F=(6x−14) ∘ , \text{m}\angle G = (4x-8)^{\circ}m∠G=(4x−8) ∘ , and \text{m}\angle H = (x+15)^{\circ}m∠H=(x+15) ∘ . Find \text{m}\angle F.M∠F.

Answer 1

`\angle F =\bold{88^\circ}`

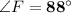
Explanation:

Given a
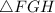`\triangle FGH` with the following angles:

`\text{m}\angle F = (6x-14)^(\circ)`

`\text{m}\angle G = (4x-8)^(\circ)`

`\text{m}\angle H = (x+15)^(\circ)`

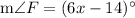
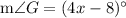
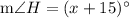
To find:

`\text{m}\angle F` = ?

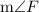Solution:

Here, we can simply use the angle sum property of a triangle to find the value of
`\text{m}\angle F`.

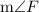As per the angle sum property of a triangle, the sum of all the interior angles a triangle is equal to
`180^\circ`.

`\angle F + \angle G + \angle H = 180^\circ`

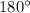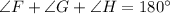
Putting all the given values in the above equation, we get:

`(6x-14)^(\circ) + (4x-8)^(\circ) + (x+15)^(\circ) = 180^\circ\\\Rightarrow 11x-7=180^\circ\\\Rightarrow 11x=180+7\\\Rightarrow 11x=187\\\Rightarrow x = \bold{17}`

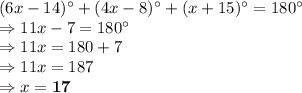
Putting the value of
`x` in
`\angle F`

`\text{m}\angle F = (6x-14)^\circ\\\Rightarrow \text{m}\angle F = (6* 17-14)^\circ\\\Rightarrow \text{m}\angle F = \bold{88^\circ}`