Answer:
a) The maximum height of the ball is 272.25 feet
b) The balls take 8 seconds to hit the ground.
Explanation:
a) You know that the quadratic function h(t)=−16*t²+124*t+32 models the ball's height about the ground, h(t), in feet, t seconds after it was thrown.
Being a quadratic function of the form:
f (x) = a*x² + b*x + c
The vertex of a quadratic or parabola equation is the highest or lowest point on the graph corresponding to that function. When a> 0, the vertex of the parabola is at the bottom of it and indicates the minimum of the function. When a <0 the vertex is at the top and indicates the maximum of the function.
The value of x at the vertex is calculated by the expression:
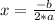
The value of y at the vertex is calculated by substituting the value of x at the vertex into the quadratic function.
In this case, being a=-16, b=124 and c=32 you get that the maximum time is:
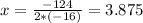
Then a maximum height of:
h(3.875)=−16*(3.875)²+124*3.875+32
h(3.875)= 272.25
The maximum height of the ball is 272.25 feet
b) When the ball hits the ground the height is zero. So h (t) = 0:
0=−16*t²+124*t+32
Applying the resolvent:
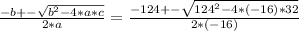
you get:
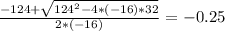
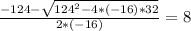
Since the time cannot be negative, the balls take 8 seconds to hit the ground.