Question

HELP PLEASE URGENT

If a 0.16 kg 8-ball at rest is hit by the 0.17 kg cue ball that is moving at a speed of 2 m/s, what is the speed of the 8-ball if the cue ball is completely stopped after the collision?

Answer 1

The speed of the 8-ball is 2.125 m/s after the collision.

Step-by-step explanation:

Law Of Conservation Of Linear Momentum

The total momentum of a system of masses is conserved unless an external force is applied. The formula for the momentum of a body with mass m and velocity v is

P=mv

If we have a system of masses, then the total momentum is the sum of them all

`P=m_1v_1+m_2v_2+...+m_nv_n`

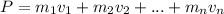
If a collision occurs, the velocities change to v' and the final momentum is:

`P'=m_1v'_1+m_2v'_2+...+m_nv'_n`

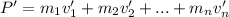
In a system of two masses, the law of conservation of linear momentum takes the form:

`m_1v_1+m_2v_2=m_1v'_1+m_2v'_2`

The m1=0.16 Kg 8-ball is initially at rest v1=0. It is hit by an m2=0.17 Kg cue ball that was moving at v2=2 m/s.

After the collision, the cue ball remains at rest v2'=0. It's required to find the final speed v1' after the collision.

The last equation is solved for v1':

`\displaystyle v'_1=(m_1v_1+m_2v_2-m_2v'_2)/(m_1)`

`\displaystyle v'_1=(0.16*0+0.17*2-0.17*0)/(0.16)`

`\displaystyle v'_1=(0.34)/(0.16)`

`v'_1=2.125\ m/s`

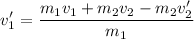
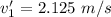
The speed of the 8-ball is 2.125 m/s after the collision.