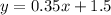Question

Write the equation of this linear relationship in slope intercept form, use decimals in your answer!! Please help

Answer 1

`y = 0.35x + 1.5`

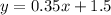
Explanation:

To write an equation to represent the linear relationship in slope-intercept form, as
`y = mx + b`, we need to determine the slope (m) and the y-intercept (b).

Find slope (m) using of the line that passes through (0, 1.5) and (100, 36.5):

`slope (m) = (y_2 - y_1)/(x_2 - x_1) = (36.5 - 1.5)/(100 - 0) = (35)/(100) = 0.35`

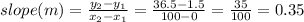
The y-intercept (b) is the value of y when x = 0. It is the point where the y-axis is intercepted. Form the table, we see that y = 1.5 when x = 0. Therefore,

y-intercept (b) = 1.5

Substitute m = 0.35, and b = 1.5 into
`y = mx + b`, to get the equation.

The equation would be:

✅
`y = 0.35x + 1.5`