-------------------------------------------------------------------------------------------------------------
Answer:
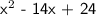
-------------------------------------------------------------------------------------------------------------
Given:

Find:
Solution: In order to determine the quadratic equation we need to move the integers onto the side where x is and then distribute.
Move the integers
Create and expression and distribute
Therefore, after completing the steps we were able to determine that the quadratic equation that will have solutions of x = 12 and x = 2 is x^2 - 14x + 24.