Question

Use the remainder theorem to determine if x = 4 is a zero of the following polynomial and find the quotient and the remainder

p(x) = x2 + 11x - 60
ОА.
Yes, x = 4 is a zero of the polynomial
The quotient is x + 15, and the remainder is 0.
ОВ.
No, x = 4 is not a zero of the polynomial
The quotient is x + 15, and the remainder is 0
OC Yes x = 4 is a zero of the polynomial.
The quotient is x + 7, and the remainder is 0
D
No, x = 4 is not a zero of the polynomial.
The quotient is x + 7, and the remainder is -88

Answer 1

Given:

The polynomial is

`p(x)=x^2+11x-60`

To find:

Whether x = 4 is a zero of the given polynomial by remainder theorem and find the quotient and remainder.

Solution:

According to the remainder theorem, if (x-c) divides a polynomial p(x), then the remainder is p(c).

Divide the polynomial by (x-4) and check whether the remainder p(x)=0 at x=4.

Putting x=4 in the given polynomial, we get

`p(4)=(4)^2+11(4)-60`

`p(4)=16+44-60`

`p(4)=60-60`

`p(4)=0`

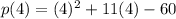
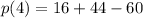
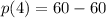
Since, remainder is 0, therefore, (x-4) is a factor of p(x) and x=4 is a zero.

Now, on dividing p(x) be (x-4) we get

`(x^2+11x-60)/(x-4)=(x^2+15x-4x-60)/(x-4)`

`(x^2+11x-60)/(x-4)=(x(x+15)-4(x+15))/(x-4)`

`(x^2+11x-60)/(x-4)=((x+15)(x-4))/(x-4)`

`(x^2+11x-60)/(x-4)=x+15`

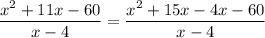
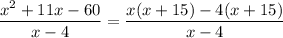
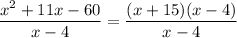
The quotient is x+15 and remainder is 0.

Therefore, the correct option is A.