Answer:
Proof below
Explanation:
To prove DE and AB are parallel, we compare the slopes of both segments
Suppose we know a line passes through points A(x1,y1) and B(x2,y2). The slope can be calculated with the equation:
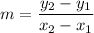
Segment AB goes through the points (0,0) and (x2,0), thus:
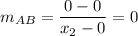
The slope is 0 because the line is horizontal.
Now for the segment DE, the endpoints are
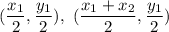
The slope is:
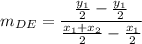
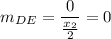
Segment DE is also horizontal, thus is parallel to segment AB.