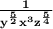Question

Can someone show me the answer and maybe the work

Answer 1

Solving the expression \frac{y^2z^{\frac{1}{4}} }{(z^{\frac{1}{2}}.xy^{\frac{3}{2}})^3} we get
`\mathbf{\frac{1}{y^{(5)/(2) }x^3z^{(5)/(4) }}}`

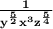
Explanation:

We need to solve the expression:

`\frac{y^2z^{(1)/(4)} }{(z^{(1)/(2)}.xy^{(3)/(2)})^3}`

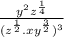
We know the exponent rule:
`(a^n)^m = a^(nm)`

`\frac{y^2z^{(1)/(4)} }{(z^{(1)/(2)}.xy^{(3)/(2)})^3}\\\\=\frac{y^2z^{(1)/(4)} }{z^{(3)/(2)}.x^3y^{(9)/(2) }}`

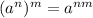
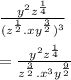
Now, another exponent rule says that:
`(a^m)/(a^n)=a^(m-n)`

`=\frac{y^{2-(9)/(2)} z^{(1)/(4)-(3)/(2) } }{x^3}\\=\frac{y^{(4-9)/(2)} z^{(1-3*2)/(4) } }{x^3}\\=\frac{y^{(-5)/(2)}z^{(-5)/(4) } }{x^3}`

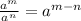
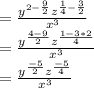
We also know that:
`a^(-m)=(1)/(a^m)`

=
`\frac{1}{y^{(5)/(2) }x^3z^{(5)/(4) }}`

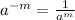
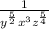
So, solving the expression \frac{y^2z^{\frac{1}{4}} }{(z^{\frac{1}{2}}.xy^{\frac{3}{2}})^3} we get
`\mathbf{\frac{1}{y^{(5)/(2) }x^3z^{(5)/(4) }}}`