Given:
A figure.
To find:
The value of x and y.
Solution:
In triangle ADC, all angles are equal, so it is an equilateral triangle.
We know that, all sides of an equilateral triangle are equal.
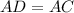 ...(i)
...(i)
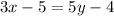 ...(ii)
...(ii)
In triangle ABD,
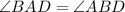
Base angles are equal, so triangle ABD is an isosceles triangle.
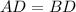 ...(iii)
...(iii)
Using (i) and (iii), we get
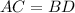
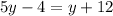
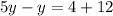

Divide both sides by 4.
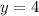
Putting y=4 in (ii), we get

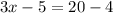
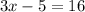
Adding 5 on both sides, we get
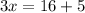
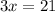
Divide both sides by 3.
[tex]x=7/tex]
Therefore, the value of x is 7 and the value of y is 4.