Answer:
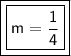
Explanation:
The slope of a line can be found using the slope formula or dividing the change in y by the change in x.
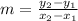
where (x₁, y₁) and (x₂, y₂) are the points the line passes through.
We are given the points (2,1) and (6,2). Therefore:
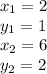
Substitute the points into the formula.
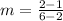
Solve the numerator.
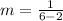
Solve the denominator
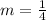
This fraction cannot be reduced further, so it is the slope. It can be written as a decimal too:
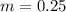
The slope of the line is 1/4 (0.25)