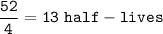13 half-lives have passed
Further explanation
General formulas used in decay:
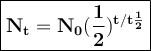
T = duration of decay
t 1/2 = half-life
N₀ = the number of initial radioactive atoms
Nt = the number of radioactive atoms left after decaying during T time
t1/2 = 4 days
Nt=18 mg (0.01% of the original isotope)
18 mg (Nt) = 0.01% No
No = the original isotope :
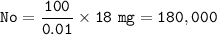
The duration of decay (T) :
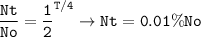

Half-lives passed :