Question

From A to Z BU

9 Love From A to Z
9 Love From A to Z
20
The
equation d = n²-12n + 43
models the number of defective
items d
produced in a manufacturing process where there
workers in a restricted
are n
area
a) solve for
When
do 30
I
b) solve for n
when
d=20

Answer 1

a) we get value of n: n=10.7 or n=1.2 when d=30

b) we get value of n: n=9.6 or n=2.3 when d=20

Explanation:

a) solve for n When do= 30

Put d= 30 in the given equation:

`d = n^2-12n + 43`

`30=n^2-12n+43\\n^2-12n+43-30=0\\n^2-12n+13=0\\`

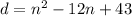
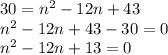
Now, we will find value of n by using quadratic formula:
`x=(-b\pm√(b^2-4ac))/(2a)`

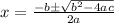
We have a=1, b=-12 and c=13

`n=(-b\pm√(b^2-4ac))/(2a)\\n=(-(-12)\pm√((-12)^2-4(1)(13)))/(2(1))\\n=(12\pm√(144-52))/(2)\\n=(12\pm√(92))/(2)\\n=(12\pm9.59)/(2)\\n=(12+9.59)/(2) , n=(12-9.59)/(2)\\n=10.7 , n=1.2\\`

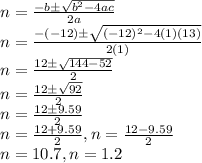
So, we get value of n: n=10.7 or n=1.2

b) solve for n when d=20

`d=n^2-12n+43\\20=n^2-12n+43\\n^2-12n+43-20=0\\n^2-12n+23=0\\`

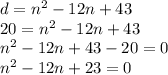
Now, we will find value of n by using quadratic formula:
`x=(-b\pm√(b^2-4ac))/(2a)`

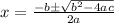
We have a=1, b=-12 and c=23

`n=(-b\pm√(b^2-4ac))/(2a)\\n=(-(-12)\pm√((-12)^2-4(1)(23)))/(2(1))\\n=(12\pm√(144-92))/(2)\\n=(12\pm√(52))/(2)\\n=(12\pm7.21)/(2)\\n=(12+7.21)/(2) , n=(12-7.21)/(2)\\n=9.6 , n=2.3\\`

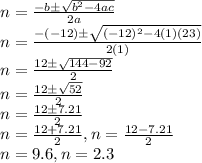
So, we get value of n: n=9.6 or n=2.3