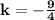Question

The function f is defined by f(x) = k/x+3, where k is a constant. Find k, if the graph of f passes through the point (3/4,0).

k=

Answer 1

The value of k if the graph of f passes through the point (3/4,0) is
`\mathbf{k=-(9)/(4)}`

Explanation:

We are given the function:
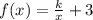`f(x)=(k)/(x)+3` where k is constant.

We need to find k, if the graph of f passes through the point (3/4,0).

So, graph passes through point (3/4,0) we have x=3/4 and y =0

Putting value of x in given function we can find value of x

We have f(x)=0, and x= 3/4

`f(x)=(k)/(x)+3\\0=(k)/((3)/(4) )+3`

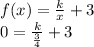
Using fraction rule:
`(a)/((b)/(c) )=(a.c)/(b)`

`0=(4k)/(3 )+3\\Taking \ LCM\\0=(4k+9)/(3)\\3*0=4k+9\\0=4k+9\\4k=-9\\k=(-9)/(4)`

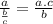
So, The value of k if the graph of f passes through the point (3/4,0) is
`\mathbf{k=-(9)/(4)}`