Question

Two spherical balls are placed so that their centers are 3.61 m apart. The

force between them is 1.65 x 10-7 N. If the mass of the smaller ball is 81 kg,
what is the mass in kilograms of the other ball?

Answer 1

The mass of the other ball is 397.775 kg.

Step-by-step explanation:

Gravitation is the force of mutual attraction that bodies experience due to the fact that they have a certain mass.

The universal law of gravitation is a classical physical law that describes the gravitational interaction between different bodies with mass.

The law was formulated by Newton, who deduced that the force with which two bodies of different masses are attracted only depends on the value of their masses and the square of the distance that separates them.

In other words, the Law of Universal Gravitation predicts that the force exerted between two bodies of masses M1 and M2 separated by a distance "d" is proportional to the product of their masses and inversely proportional to the square of the distance, that is:

`F=G(M1*M2)/(d^(2) )`

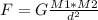
where:

• F = It is the module of the force exerted between both bodies, and its direction is found on the axis that joins both bodies.

• G = It is the constant of Universal Gravitation, whose value is 6.67384*10⁻¹¹
  `(N*m^(2) )/(kg^(2) )`

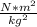
In this case:

• F= 1.65*10⁻⁷ N

• G= 6.67384*10⁻¹¹
  `(N*m^(2) )/(kg^(2) )`

• M1= 81 kg
• M2= ?
• d= 3.61 m

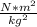
Replacing:

`1.65*10^(-7) N=6.67384*10^(-11) (N*m^(2) )/(kg^(2) )(81 kg*M2)/((3.61 m)^(2) )`

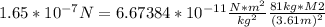
Solving for M2:

`M2=(1.65*10^(-7) N*(3.61 m)^(2))/(6.67384*10^(-11) (N*m^(2) )/(kg^(2) )*81 kg)`

M2= 397.775 kg

The mass of the other ball is 397.775 kg.