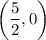Question

Inverse of f(x)=2 1/2-3 1/3x and what is its x intercept

Answer 1

Find appropriate f(x) first

• 2 1/2=5/2
• 3 1/3=10/3

Now

• y=-10/3x+5/2

So

InterchAnge x and y

• x=-10/3y+5/2

Find y which is the inverse

• x-5/2=-10/3y
• y=-3/10x+5/2×3/10
• y=-3/10x+3/4

x intercept

• 10/3x+3/4=0
• x=-3/4×3/10
• x=-9/40

Graph attached

Answer 2

`\textsf{Inverse function}: \quad f^(-1)(x)=(3)/(4)-(3)/(10)x`

`x\textsf{-intercept}:\quad\left((5)/(2),0\right)`

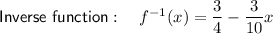
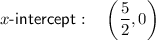
Explanation:

Given:

`f(x)=2(1)/(2)-3(1)/(3)x`

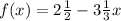
Rewrite the function so it is a rational function

Convert the mixed numbers to improper fractions:

`\implies f(x)=(5)/(2)-(10x)/(3)`

Make the denominators the same:

`\implies f(x)=(3 \cdot 5)/(3\cdot 2)-(2 \cdot 10x)/(2 \cdot 3)`

`\implies f(x)=(15)/(6)-(20x)/(6)`

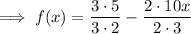
Combine:

`\implies f(x)=(15-20x)/(6)`

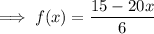
The inverse of a function is its reflection in the line y = x

To find the inverse, make x the subject

Replace f(x) with y:

`\implies y=(15-20x)/(6)`

`\implies 6y=15-20x`

`\implies 6y-15=-20x`

`\implies x=(-6y+15)/(20)`

`\implies x=(15-6y)/(20)`

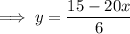
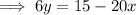
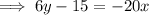
Replace x with
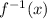`f^(-1)(x)` and y with x:

`\implies f^(-1)(x)=(15-6x)/(20)`

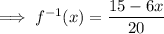
If necessary, convert back into the same format as the original function:

`\implies f^(-1)(x)=(15)/(20)-(6x)/(20)`

`\implies f^(-1)(x)=(3)/(4)-(3)/(10)x`

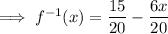
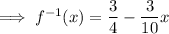
The x-intercept of the inverse function is the point at which it crosses the x-axis, so when
`f^(-1)(x)=0`

`\implies (15-6x)/(20)=0`

`\implies 15-6x=0`

`\implies 6x=15`

`\implies x=(15)/(6)=(5)/(2)`

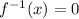
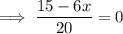
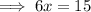
Therefore, the x-intercept is:

`\left((5)/(2),0\right)`