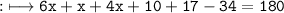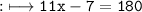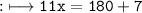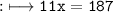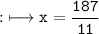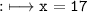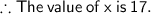Question

What is the value of x? There is isosceles triangle. The measure of angle which is between two congruent sides is (6x+10⁰). The measures of other angles are (x+17⁰) and (4x-34⁰).

Answer 1

Answer:-

x=17

step-by-step Step-by-step explanation:-

`{\boxed{\quad\:\mapsto\rm Firstly\:Let's\:understand\:the\:concept:-}}`

This is a isosceles triangle. As it is a triangle we can apply sum theory. we have to take the sum of given unknown polynomials as 180° .Then by solving it we can find the value of x.

Solution:-

Given angles

• (6x+10°)
• (x+17°)
• (4x-34)°

According to sum theory

`{\boxed{\sf The \:sum\:of\:angles=180°}}`

• Substitute the values

`\qquad \quad{:}\longmapsto\tt (6x+10)+(x+17)+(4x-34)=180`

• Remove brackets

`\qquad \quad{:}\longmapsto\tt 6x+10+x+17+4x-34=180`

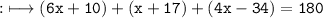
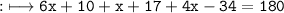
• Together like polynomials and constants

`\qquad \quad{:}\longmapsto\tt 6x+x+4x+10+17-34=180`

`\qquad \quad{:}\longmapsto\tt 11x-7=180`

• Interchange sides

`\qquad \quad{:}\longmapsto\tt 11x=180+7`

`\qquad \quad{:}\longmapsto\tt 11x=187`

`\qquad \quad{:}\longmapsto\tt x=\cancel{(187)/(11)}`

• Simplify

`\qquad \quad{:}\longmapsto\tt x=17`

`\therefore\sf The \:value\:of\:x\;is\:17.`