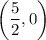Answer:
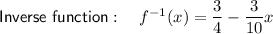
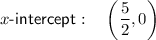
Explanation:
Given:
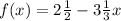
Rewrite the function so it is a rational function
Convert the mixed numbers to improper fractions:
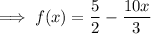
Make the denominators the same:
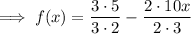
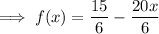
Combine:
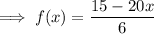
The inverse of a function is its reflection in the line y = x
To find the inverse, make x the subject
Replace f(x) with y:
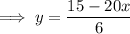
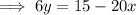
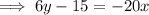
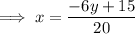
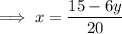
Replace x with
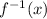 and y with x:
and y with x:
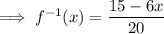
If necessary, convert back into the same format as the original function:
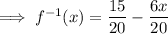
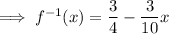
The x-intercept of the inverse function is the point at which it crosses the x-axis, so when
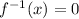
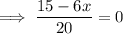

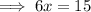
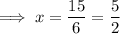
Therefore, the x-intercept is: