Marc's conclusion is that the mean age of the prison population in his city is not significantly less than 26 years based on the given sample.
How to determine Marc's conclusion
To determine Marc's conclusion regarding the mean age of the prison population in his city, conduct a hypothesis test using the given information and the significance level of 0.05.
Let's set up the null and alternative hypotheses:
Null hypothesis (H0): The mean age of the prison population is equal to or greater than 26 years.
Alternative hypothesis (Ha): The mean age of the prison population is less than 26 years.
Use a one-sample t-test to test these hypotheses.
Given that the sample size is 25 and the sample mean is 24.4 years, calculate the t-statistic using the formula:
t = (sample mean - hypothesized mean) / (sample standard deviation / sqrt(sample size))
t = (24.4 - 26) / (9.2 /
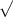 (25))
(25))
t = -1.6 / (9.2 / 5)
t = -1.6 / 1.84
t ≈ -0.87
Next, determine the critical t-value based on the significance level and degrees of freedom (df = sample size - 1 = 25 - 1 = 24).
At a significance level of 0.05 and 24 df, the critical t-value is approximately -1.711.
Since the calculated t-value (-0.87) is greater than the critical t-value (-1.711), we fail to reject the null hypothesis. This means that there is not enough evidence to conclude that the mean age of the prison population is less than 26 years at a significance level of 0.05.
Therefore, Marc's conclusion is that the mean age of the prison population in his city is not significantly less than 26 years based on the given sample.