Answer:
x = 2 and x = 5
Explanation:
What are the roots of an equation?
In simple terms, the roots are simply the x intercepts of an equation.
How to find the roots of a quadratic equation:
We can find the roots of a quadratic equation one of three ways. Here you will learn how to do all three ways.
The first way (easiest way) :
The first way to find the roots of a quadratic equation is to graph the equation on a calculator and find where the equation crosses the x axis ( these are the x intercepts )
If you look at the attached image, you see the given equation x² - 7x + 10 = 0 graphed. The equation passes the x axis at (2,0) and (5,0) meaning the roots are x = 2 and x = 5.
Second way : Using the quadratic formula:
If you don't have a calculator or don't know how to graph the equation this is the best alternative way to find the roots.
The quadratic formula is :
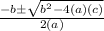
Where the values of a,b and c are derived from the quadratic equation which should be written in quadratic form : ax² + bx + c = 0
This is the case here so we can easily define our variables and plug them into our formula
We have "ax² + bx + c = 0" = x² - 7x + 10 = 0 so we can say a = 1 , b = -7 and c = 10
We now plug these into the formula
Recall formula :
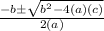
==> plug in a = 1 , b = -7 and c = 10
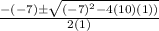
==> remove parenthesis from -(-7)

==> simplify exponents
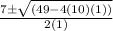
==> simplify all multiplication
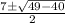
==> subtract 40 from 49
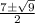
==> simplify sqrt

==> simplify +/-
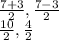
==> simplify division
5 , 2
The roots are x = 5 and x = 2
( Note that we used BPEMDAS to evaluate the formula when the values of a,b and c were plugged in. BPEMDAS is simply folllowing an order of operations to ensure you get the right answer. The order is as follows : Brackets , Parenthesis (any operations inside of parenthesis) , Exponents , Multiplication and Division ( do in order going left to right ) , Addition and Subtract ( do in order going left to right )
Also note that the quadratic formula ALWAYS WORKS.
Last way: Factoring
Finally, we can also find the roots by factoring.
We have x² - 7x + 10 = 0
We must first find a number that multiplies to 10 and adds to -7
We can do so by listing the factors of 10
Factors of 10 include , 10 and 1 , -10 and -1 , -5 and -2, and 5 and 2
Out of these we want to find the multiples that add to -7
10 + 1 = 11
-10 + -1 = -11
-5 + - 2 = -7
5 + 2 = 7
The multiples that add to -7 are -5 and -2 .
From there we want to split the -7 and x² to get (x-5)(x-2)
We then solve the roots by setting the individual factors to 0
x - 5 = 0
==> add 5 to both sides
x = 5
x - 2 = 0
==> add 2 to both sides
x = 2