Question

I need help!! please

Answer 1

Answer: 40

========================================================

Step-by-step explanation:

The old dimensions of the rectangle were 30 by 15.

The new dimensions are 30+x by 15+x, where x is some positive number.

The new rectangle dimensions multiply to 1000

(30+x)(15+x) = 1000

Use the FOIL rule to expand out the left side like so

(30+x)(15+x) = 1000

450+30x+15x+x^2 = 1000

450+45x+x^2 = 1000

x^2+45x+450

Then lets get everything to one side

x^2+45x+450 = 1000

x^2+45x+450-1000 = 0

x^2+45x-550 = 0

---------------------

From here we use the quadratic formula

Plug in a = 1, b = 45, and c = -550.

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-(45)\pm√((45)^2-4(1)(-550)))/(2(1))\\\\x = (-45\pm√(4225))/(2)\\\\`

`x = (-45\pm65)/(2)\\\\x = (-45+65)/(2) \ \text{ or } \ x = (-45-65)/(2)\\\\x = (20)/(2) \ \text{ or } \ x = (-110)/(2)\\\\x = 10 \ \text{ or } \ x = -55\\\\`

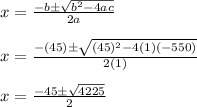
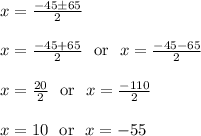
Earlier we defined x to be a positive number. This means we ignore x = -55. It makes no sense to add on a negative amount to each dimension.

The only practical answer is x = 10.

So each dimension is increased by 10 feet.

--------------------------

If x = 10, then the old dimensions of 30 by 15 bump up to 30+10 = 40 by 15+10 = 25

Then note how 40*25 = 1000, which helps confirm we have the correct dimensions.

--------------------------

Now go back to the question at hand: we want to find the new width. The old width was 30 feet. The new width is 30+x = 30+10 = 40 feet