Answer:(C)2Step-by-step explanation:Given the polynomial:
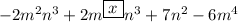 where x is the missing exponent.We desire our polynomial to be a binomial (have two terms) after simplification.We observe that the first and second term are positive and negative of almost the same term.Therefore, we rewrite the polynomial in such a way that the first and second term cancels out.This is:[tex]-2m^2n^3 + 2m^{\boxed{2}}n^3 + 7n^2 - 6m^4\$Simplified, we have:\\=7n^2 - 6m^4 Therefore, the missing exponent on the m in the second term is 2.
where x is the missing exponent.We desire our polynomial to be a binomial (have two terms) after simplification.We observe that the first and second term are positive and negative of almost the same term.Therefore, we rewrite the polynomial in such a way that the first and second term cancels out.This is:[tex]-2m^2n^3 + 2m^{\boxed{2}}n^3 + 7n^2 - 6m^4\$Simplified, we have:\\=7n^2 - 6m^4 Therefore, the missing exponent on the m in the second term is 2.
Explanation: