Question

PLSS HELPPPP MEE ITS DUE TMRW

Answer 1

a) (-2 , -1)

b) (-1 , 0) and (-3 , 0)

Explanation:

For part a)

We can find the coordinates of the turning point by seeing at the graph where it turns the other way or in simpler words the axis of symmetry so if see the graph the axis of symmetry is the line x = -2 so that means the turning point is (-2 , -1).

For finding the turning point mathematically we compare the equation to its standard form which is:

`x^2+4x+3=a(x-h)^2+k`

where h is the x coordinate and k is the y coordinate of the turning point of the equation (h , k) = (x , y).

so just solve the left side,

`a(x-h)^2+k\\a((x)^2-2(x)(h)+(h)^2)+k\\a(x^2-2xh+h^2)+k\\\\ax^2-2ahx+ah^2+k=x^2+4x+3\\`

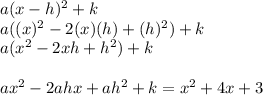
and so we compare the coefficients of x^2 on the right and left side we get

`a=1`

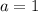
if we compare the coefficients of x on the right and left side we get

`-2ah=4\\-2(1)h=4\\-2h=4\\h=(4)/(-2)\\\\h=-2`

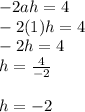
now we compare the constants on the right and left side we get

`ah^2+k=3\\(1)(-2)^2+k=3\\(1)(4)+k=3\\4+k=3\\k=3-4\\k=-1`

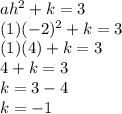
so the turning point is (-2 , -1) proven mathematically and graphically as well

For part b)

Roots of the equation are also called as x-intercepts which means where the graph intersects/cuts the x-axis so if see the graph it cuts the x-axis at 2 points firstly at -3 and then at -1 so the roots of the equation would be (-1 , 0) and

(-3 , 0) the y coordinate is zero when the points lies on the x-axis.

for mathematically solving the equation we would equate the equation to zero

`y=x^2+4x+3\\x^2+4x+3=0`

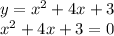
Now solve it by either factorizing or by using the quadratic formula we would get two values for x those are the roots of the equation

we solve it by factoring

`x^2+4x+3=0\\x^2+3x+x+3=0\\x(x+3)+1(x+3)=0\\(x+3)(x+1)=0\\x=-3\ ,\ x=-1\\`

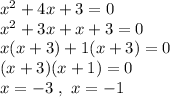
proven mathematically as well as graphically.

Answer 2

the turning point is (-2,-1)

i dont know the turning point but i hope this helps

Explanation: