Question

Please solve the following differential equation:
​

Answer 1

Solve the corresponding homogeneous equation:

`y'' = 0`

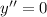
Integrate twice to get the characteristic solution:

`\displaystyle \int (d^2y)/(dt^2) \, dt = \int 0 \, dt \implies (dy)/(dt) = C_1`

`\displaystyle \int (dy)/(dt) \, dt = \int C_1 \, dt \implies y = C_1 t + C_2`

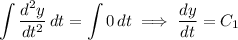
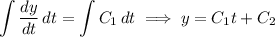
For the particular solution, consider the ansatz

`y = a e^(-2t) + b e^(4t)`

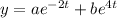
with second derivative

`y'' = 4a e^(-2t) + 16 be^(4t)`

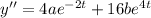
Substitute this into the differential equation and solve for the unknown coefficients.

`4a e^(-2t) + 16 be^(4t) = e^(-2t) + 10e^(4t)`

`\implies \begin{cases}4a = 1 \\ 16b = 10\end{cases} \implies a = \frac14, b = \frac58`

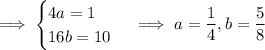
The general solution is then

`y = C_1 t + C_2 + \frac14 e^(-2t) + \frac58 e^(4t)`

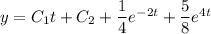
with first derivative

`y' = C_1 - \frac12 e^(-2t) + \frac52 e^(4t)`

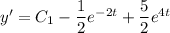
Use the initial conditions to solve for the remaining constants.

`y(0) = 1 \implies 1 = C_2 + \frac14 + \frac58 \implies C_2 = \frac18`

`y'(0) = 0 \implies 0 = C_1 - \frac12 + \frac52 \implies C_1 = -2`

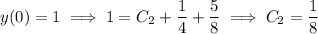
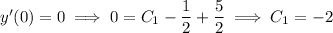
Then the particular solution to the initial value problem is

`\boxed{y = -2t + \frac18 + \frac14 e^(-2t) + \frac58 e^(4t)}`

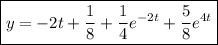
(A)