Question

Jim wants to make 2.7 quarts of a 60% alcohol solution by mixing together a 80% alcohol solution and a 20% alcohol solution. How much of each solution must Jim use?

Answer 1

1.8 quartz of 80% solution and

0.9 quarts of 20% solution.

Explanation:

Given that:

Total alcohol solution to be made = 2.7 quarts of 60% solution

Alcohol concentration in first solution= 80%

Alcohol concentration in second solution = 20%

To find:

How much of each solution must Jim use?

Solution:

Let amount of first solution to be used =
`x` quartz

Total amount is given as = 2.7 quarts

So, amount of second solution to be used = (2.7 -
`x`) quartz

As per question statement, we can write the following equation:

`80\%\ of\ x +20\%\ of\ (2.7-x) = 60\%\ of\ 2.7\\\Rightarrow (80)/(100) x +(20)/(100) (2.7-x) = (60)/(100)* 2.7\\\Rightarrow 4x+2.7-x =3* 2.7\\\Rightarrow 3x=2* 2.7\\\Rightarrow \bold{x =1.8\ quartz}`

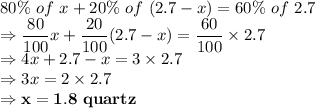
First solution, 80% solution to be used = 1.8 quartz

Second solution, 20% solution to be used = 2.7 - 1.8 = 0.9 quartz