Question

What is the range of the function f(x)= square root of x-8+6

Answer 1

Range = [6, ∞)

Explanation:

The range of a function is its output values (y-values).

One way to find the range of the given function is to determine the series of translations that have transformed the given function from the parent function.

Translations

For a > 0

`f(x+a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units left}`

`f(x-a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units right}`

`f(x)+a \implies f(x) \: \textsf{translated}\:a\:\textsf{units up}`

`f(x)-a \implies f(x) \: \textsf{translated}\:a\:\textsf{units down}`

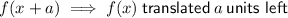
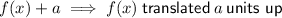
Parent function:
`f(x)=√(x)`

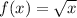
• Domain: [0, ∞)
• Range: [0, ∞)

Given function:
`f(x)=√(x-8)+6`

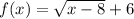
The parent function has been:

Translated 8 units right:
`f(x-8)=√(x-8)`

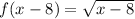
then translated 6 units up:
`f(x-8)+6=√(x-8)+6`

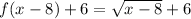
If the function has been translated 8 units right, the domain will be:

• Domain: [0 + 8, ∞) = [8, ∞)

Similarly, if the function has been translated 6 units up, the range will be:

• Range: [0 + 6, ∞) = [6, ∞)

Answer 2

• The range of the given function is [6, + ∞)

Explanation:

It is assumed the function is:

• 
  `f(x)=√(x-8) +6`

We know the square root is non-negative, so:

• x - 8 ≥ 0 therefore the function gets values

• f(x) ≥ 0 + 6
• f(x) ≥ 6

We can show this as:

• f(x) ∈ [6, + ∞)