Question

A box in a certain supply room contains three 40-w lightbulbs, five 60-w bulbs, and seven 75-w bulbs. suppose that three bulbs are randomly selected. (round your answers to four decimal places.) (d) suppose now that bulbs are to be selected one by one until a 75-w bulb is found. what is the probability that it is necessary to examine at least six bulbs?

Answer 1

0.0186

Step-by-step explanation:

Given that there are 8 bulbs we don't want (3+5=8), and 7 bulbs we do want, there are 15 bulbs total.

If we are selecting bulbs one at a time, and we're looking for the probability that we don't find a bulb until at least the sixth try, we didn't find the right bulb on the first 5 tries. On the 6th try, we might have found the right bulb, or maybe we didn't and needed more tries, but we know that we must have missed on the first 5 tries.

So, we want the following probability:

`P({1^(st)}_{\text{wrong}})*P({2^(nd)}_{\text{wrong}})*P({3^(rd)}_{\text{wrong}})*P({4^(th)}_{\text{wrong}})*P({5^(th)}_{\text{wrong}})*P({6^(th)}_{\text{right or wrong}})`

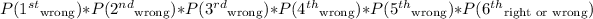
At any point, the probability of choosing the wrong bulb is
`\frac{\text{\# wrong bulbs left}}{\text{\# bulbs left}}`

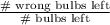
Also, at any point, the probability of choosing a right or a wrong bulb is
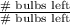`\frac{\text{\# bulbs left}}{\text{\# bulbs left}}` which is equivalent to 1 . If you choose a bulb, you either chose a right one, or a wrong one, there's no other choice.

So, the probability we're looking for is as follows:

`P({1^(st)}_{\text{wrong}})*P({2^(nd)}_{\text{wrong}})*P({3^(rd)}_{\text{wrong}})*P({4^(th)}_{\text{wrong}})*P({5^(th)}_{\text{wrong}})*P({6^(th)}_{\text{right or wrong}})`
`(8)/(15)*(7)/(14)*(6)/(13)*(5)/(12)*(4)/(11)*(10)/(10)`

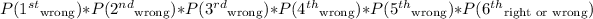
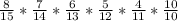
0.0186480186

So, there is a 1.8648% chance of picking the correct bulb on the 6th try of later. In terms of probability, the probability (to 4 decimal places) is 0.0186