Solve the corresponding homogeneous equation:
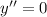
Integrate twice to get the characteristic solution:
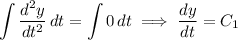
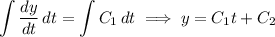
For the particular solution, consider the ansatz
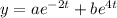
with second derivative
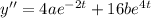
Substitute this into the differential equation and solve for the unknown coefficients.
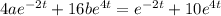
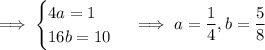
The general solution is then
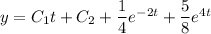
with first derivative
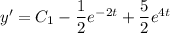
Use the initial conditions to solve for the remaining constants.
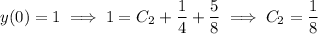
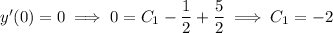
Then the particular solution to the initial value problem is
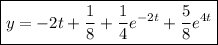
(A)