Question

Consider the quadratic function: y = 2x^2 + 7x + 10

What is the y-intercept? [Select]

Does the function open up or down? (Select]

Does the function have a maximum or a minimum? [Select ]

Answer 1

y-intercept: 10

concavity: function opens up

min/max: min

Explanation:

1.) The definition of a y-intercept is what the resulting value of a function is when x is equal to 0.

Therefore, if the function's equation is given, to find y-intercept simply plug in 0 for the x-values:

`y = 2x^2+7x+10 = 2(0)^2 + 7(0)+10 = 2(0) + 0 + 10 = 0 + 10 = 10`

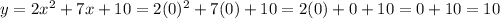
y intercept ( f(0) )= 10

2.) In order to find concavity (whether a function opens up or down) of a quadratic function, you can simply find the sign associated with the x^2 value. Since 2x^2 is positive, the concavity is positive. This is basically possible, since it is identifying any reflections affecting the y-values / horizontal reflections.

3.) In order to find whether a quadratic function has a maximum or minimum, you can use the concavity of the function. The idea is that if the function opens downwards, the vertex would be at the very top, resulting in a maximum. If a function was open upwards, the vertex would be at the very bottom, meaning there is a minimum. Like the concavity, if the value associated with x^2 is positive, there is a minimum. If it is negative, there is a maximum. Since 2x^2 is positive, the function has a minimum.