Answers:
4a.)

4b.)
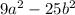
4c.)
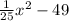
5b.)
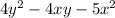
Solution Steps:
__________________________________
4a.)
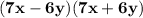 :
:
- Multiplication can be transformed into difference of squares using the rule:
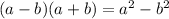 .
.
- So change the equation using the rule:
- Expand
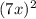 and
and
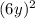 :
:
- Calculate
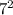 and
and
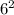 :
:
So the end equation would be:
 .
.
4b.)
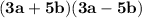 :
:
- Multiplication can be transformed into difference of squares using the rule:
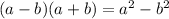 .
.
- So change the equation using the rule:
- Expand
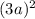 and
and
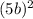 :
:
- Calculate
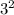 and
and
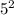 :
:
So the end equation would be:
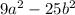 .
.
4c.)
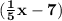 ×
×
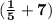 :
:
- Multiplication can be transformed into difference of squares using the rule:
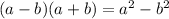 .
.
- So change the equation using the rule:
- Expand
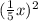 :
:
- Calculate
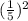 and
and
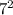 :
:
So the end equation would be:
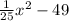 .
.
5b.)
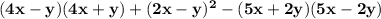 :
:
- Consider
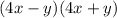 . Multiplication can be transformed into difference of squares using the rule:
. Multiplication can be transformed into difference of squares using the rule:
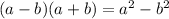 .
.
- So change the equation using the rule:
- Expand
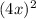 :
:
- Calculate
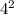 :
:
- Use binomial theorem
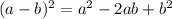 to expand
to expand
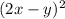 :
:
- Combine
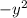 and
and
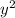 :
:
- Consider
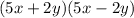 . Multiplication can be transformed into difference of squares using the rule:
. Multiplication can be transformed into difference of squares using the rule:
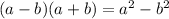 .
.
So change the equation using the rule:
- Expand
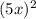 and
and
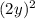 :
:
- Calculate
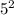 and
and
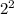 :
:
- Combine
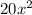 and
and
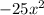 :
:
So the end equation would be:
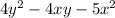 .
.
__________________________________