Question

Y= 1/3 |x-4| +15 ; x= -8

Answer 1

`\boxed{y=19}`

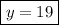
Solution Steps:

__________________________________

1.) Subtract 4 from −8:

• 
  `4-(-8)=-12`

- Since
`x=-8`, you add that into the equation.

- You subtract first because
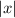`|x|` acts as parenthesis, and you always solve parenthesis first.

Equation at the end of Step 1:

• 
  `y=(1)/(3)|-12|+15`

2.) Find the absolute value of -12:

• 
  `|-12|=12`

- The absolute value of a real number
`a` is
`a` ≥
`0`, or
`-a` when
`a` <
`0`.

- So this means that if it's a positive number, the absolute value would be that same number. And if the number is negative then it'd be the positive version of the number.

Equation at the end of Step 2:

• 
  `y=(1)/(3)` ×
  `12+15`

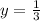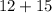
3.) Multiply
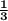`\bold{(1)/(3)}` and 12:

• 
  `(1)/(3)` ×
  `12=(12)/(3)`

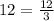
- This turns into a fraction because when you multiply a fraction by a whole number it still stays in fraction form.

Equation at the end of Step 3:

• 
  `y=(12)/(3)+15`

4.) Divide 12 by 3:

• 
  `12` ÷
  `3=4`

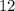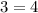
- In this part of the problem we need to get rid of the fraction and the only way to do so is to divide the numerator by the denominator.

Equation at the end of Step 4:

• 
  `y=4+15`

5.) Add 4 and 15:

• 
  `4+15=19`

- We add because there is only 2 numbers left, so those 2 numbers together will equal
`y`.

__________________________________

Answer 2

19

Explanation: