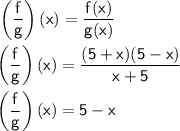Question

Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.

Answer 1

5 - x

Explanation:

Given:

`f(x)=25-x^2`

`g(x)=x+5`

`\begin{aligned}\left((f)/(g)\right)(x) & = (f(x))/(g(x))\\\\ & = (25-x^2)/(x+5)\\\\& = ((5-x)(5+x))/((x+5))\\\\& = ((5-x)(x+5))/((x+5))\\\\& = 5-x\end{aligned}`

Answer 2

`\sf \left((f)/(g)\right)(x)=5-x`

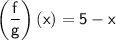
Explanation:

Given functions:

f(x) = 25 - x²

g(x) = x + 5

Difference of Perfect Squares rule: a² - b² = (a + b)×(a - b)

1. Rewrite function f(x) using the rule:

5 × 5 = 25 ⇒ 5²

x × x = x²

f(x) = 5² - x² ⇒ f(x) = (5 + x)×(5 - x)

2. Divide and simplify:

`\sf\left((f)/(g)\right)(x) =(f(x))/(g(x))\\\\\left((f)/(g)\right)(x)=((5 + x)(5 - x))/(x+5)\\\\\left((f)/(g)\right)(x)=5-x`