Question

Find the center and radius of the circle

represented by the equation below.
x² + y² - 6x + 4y+4= 0
Center:

Answer 1

Provided Equation

• x² + y² - 6x + 4y + 4= 0

As we know the Standard Equation of a Circle is

`\bf{(x - a)} {}^(2) + (y - b) {}^(2) = {r}^(2)`

where,

r radius of circle.

(a,b) centre .

`\implies \sf \: {x}^(2) + {y}^(2) - 6x + 4y + 4 = 0`

This equation can be further written as

`\implies \sf \: {x}^(2) - 6x + {y}^(2) + 4y = - 4`

Now completing the square ( by adding 4 & 9 on both side ) .

`\implies \sf \: {x}^(2) - 6x + 9 + {y}^(2) + 4y + 4 = - 4 + 9 + 4`

again this equation can be further written as

`\implies \sf \: (x - 3) {}^(2) + (y + 2) {}^(2) = {3}^(2)`

Now comparing this equation with standard equation of circle ( mentioned above) and we will get

• Centre = ( a,b) = (3, -2 )
• Radius = r = 3

Therefore,

• Centre of circle is (3,-2) and radius is 3

Answer 2

Centre:

• The general formula for the circumference is:

`\boxed{ \boxed{{x^(2) \: + \: y ^(2) \: + \: Dx \: + \: Ey \: + F \: = \: 0}}}`

________________________

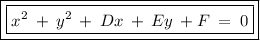
To find the center, write this formula:

`\boxed{ \boxed{C( (-D)/(2) , (-E)/(2) )}}`

____________________

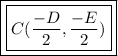
We know that...

`D \: = \: -6 \\ E \: = \: 4 \\ F \: = \: 4`

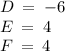
We use the equation of the center with the values already obtained:

`C( (- - 6)/(2) , (-4)/(2) )`

`C( (6)/(2) , (-4)/(2) )`

`\huge\boxed{ \bold{C( 3, - 2 )}}`

_____________________

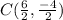
Ratio:

Now we use the equation of the radius for a circumference, which is:

`\boxed{ \boxed{{r \: = \: (1)/(2) \sqrt{D ^(2) \: + \: E ^(2) \: - \: 4F } }}}`

___________________________

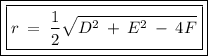
Now we use the equation of the radius for a circumference with the values already obtained.

`r \: = \: (1)/(2) \sqrt{ { - 6}^(2) \: + \: {4}^(2) \: - \: 4 \: * \: 4 }`

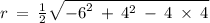
• I am going to use complex numbers because the square root of a negative number does not exist in the set of real numbers.

`r \: = \: (1)/(2) \sqrt{ { - 6}^(2) \: - \: {4}^(2) \: - + \: 4 \: * \: 4 i}`

`r \: = \: (1)/(2) \sqrt{ { 6}^(2) \: - \: {4}^(2) \: + \: 16i}`

`r \: = \: \frac{ \sqrt{ {6}^(2) \: - \: {4}^(2) \: + \: 16i} }{2}`

`r \: = \: ( √(36 \: - \: 16 \: + \: 16i) )/(2)`

`r \: = \: ( √(36i) )/(2)`

`r \: = \: (6i)/(2)`

`\huge \boxed{ \bold{r \: = \: 3i}}`

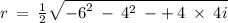
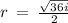
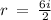
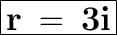
MissSpanish