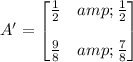Question

Help with this linear algebra question

Answer 1

Check what the transformation does for each vector in the standard basis of R² :

T (1, 0) = (5, 2)

T (0, 1) = (-4, 0)

Now compute the weights a, b and c, d such that

a T (1, 0) + b T (0, 1) = (-2, 1)

c T (1, 0) + d T (0, 1) = (-1, 1)

`\left[\begin{array}c5&-4&-2\\2&0&1\end{array}\right]\sim\left[\begin{array}cc1&0&\frac12\\\\0&1&\frac98\end{array}\right]\implies a=\frac12,b=\frac98`

`\left[\begin{array}cc5&-4&-1\\2&0&1\end{array}\right]\sim\left[\begin{array}c1&0&\frac12\\\\0&1&\frac78\end{array}\right]\implies c=\frac12,d=\frac78`

Then the matrix A' is

`A'=\begin{bmatrix}\frac12&\frac12\\\\\frac98&\frac78\end{bmatrix}`