Question

find the function P defined by a polynomial of degree 3 with real coefficients that satisfy the given conditions. The zeros are -​3,-​1, and 4. The leading coefficient is -4.

Answer 1

Given:

Degree of polynomial = 3

Zeros are -​3,-​1, and 4.

The leading coefficient is -4.

To find:

The polynomial.

Solution:

The general form of a polynomial is

`P(x)=a(x-c_1)^(m_1)(x-c_2)^(m_2)...(x-c_n)^(m_n)`

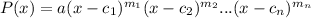
where, a is a constant,
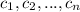`c_1,c_2,...,c_n` are zeros with multiplicity
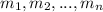`m_1,m_2,...,m_n` respectively.

Zeros of the polynomial are -​3,-​1, and 4. So,

`P(x)=a(x-(-3))(x-(-1))(x-4)`

`P(x)=a(x+3)(x+1)(x-4)`

`P(x)=a(x^2+3x+x+3)(x-4)`

`P(x)=a(x^2+4x+3)(x-4)`

`P(x)=a(x^3+4x^2+3x-4x^2-16x-12)`

`P(x)=a(x^3-13x-12)`

`P(x)=ax^3-13ax-12a`

Here, leading coefficient is a.

The leading coefficient is -4. So, a=-4.

`P(x)=(-4)x^3-13(-4)x-12(-4)`

`P(x)=-4x^3+52x+48`

Therefore, the required polynomial is
`P(x)=-4x^3+52x+48`.